ゲンツェンとの関係

あまり知られていないがシーケント計算や自然演繹を考え出したゲンツェンの最初の論文はパウル・ヘルツの体系に関する結果である¹。ヘルツは特にシーケント、カット規則、弱化規則に関してゲンツェンに影響を与えている。

この記事ではヘルツの論理システム²をより現代的な視点で見てみる。主に問題にするテキストは末尾の参考文献にあるHerz (1923)であり、必要に応じて他のテキストも参照した。

射としての含意

ヘルツの体系では命題は次の形をしている。

$(a_1, \dots, a_n)\to b$

ここでヘルツの用いる矢印は帰結関係 $\vdash$ としての役割と論理結合子としての役割が明確に区別されておらず渾然としている。論理結合子の概念をより明確化しシーケントの概念と分離させたのはゲンツェンの功績である。

$a, b$ 等は要素と呼ばれる。前件は複数で後件は一つである。Part Iである論文では前件が1つの場合に限定されており、Part II ではより一般的に複数の前件が扱われる。前件が1つの場合は次のようになる。

$a\to b$

ヘルツが次の図式を公理システムの例として挙げている。

これは $a\to b$ と $b\to c$ から $a\to c$ が得られるのに対応している。

この図を見て何か気づかないだろうか?

そう。これは圏論での射の合成の図と同じなのである。 $f: a\to b$ と $g: b\to c$ から $g\circ f: a\to c$ が得られることと同じである。ただし圏論的論理学では前件と後件の間の帰結関係 $\vdash$ が射として扱われる。

三段論法はカット規則の特殊な場合であり、カット規則は圏論的論理学では射の合成と考えられることから、このことは別に何の不思議もない。実際ヘルツはカット規則(ゲンツェンでは"Schnitt"(カット))のことをSyllogismus(シュロギスム)やunmittelbarer Schluss(直接推論)と呼んでいる。

しかしヘルツの体系は圏とは異なり恒等射の存在は含まれていない。よって圏から恒等射に関する公理を取り除いたものとなる³。

ヘルツは注1で命題 $a\to b$ はWhitehead-Russell(1900)の意味での含意に異ならないと述べている(Principia Mathematicaで1910年の誤り?)。Whitehead-Russellは含意には矢印ではなく別の記号を用いており、含意を矢印として捉えるのは彼らに由来した考えではない。

ヘルツ自身含意の解釈についてはこの論文ではIntroductionで扱う必要がないと述べており、また論文によって複数の異なる解釈を提示している。

(1) 要素をeventsとして解釈⁴。

(2) Elementsを属性として解釈。事物が属性全部 $a_1, a_2, \dots, a_n$ を満たすならば、属性 $b$ も満たす。

(3) 命題 $a\to b$ をホワイトヘッド&ラッセルの意味で解釈。

この論文でのヘルツのシステムは非常にプリミティブだが、それゆえに直接に射の合成のなすシステムように考えることが可能なのである。ゲンツェンの自然演繹やシーケント計算を圏論的に捉えることは証明図であるのでこう簡単にはいかないのだから。

分解対象としての論理結合子

ヘルツは論理結合子のようなものは扱っているが、それはゲンツェンのものとは異なり非常に奇妙なものである。

ヘルツはIdeal Elementという名前で論理結合子⁵を次のような図を用いて説明する。

この図⁶で論理結合子に相当するのは右図4bの中央の丸印である。四章の説明も合わせると以下のように説明できる。

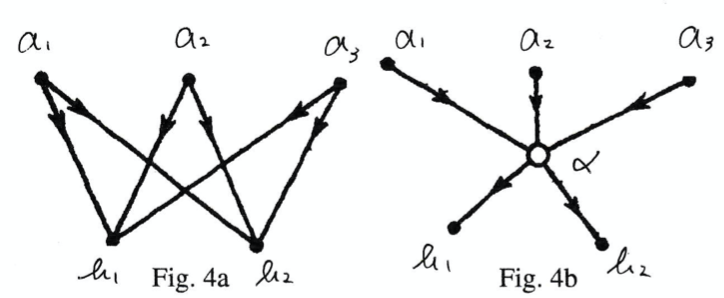
左図では計6つの辺がある。これはシステムに要素 $a_1\to b_1$ 等6つの命題があることに対応している。右図では上側の各頂点からの矢印が中央の丸印 $\alpha$ を通過し、下側の頂点に至っている。そして辺の総数は5つに減っている。つまりideal elementを導入することにより、システムに含まれるsentenceの個数が減少する。そしてヘルツはそのような目的でこのような要素を導入している。ヘルツは「このようなideal elementの唯一の役割はreal elementからなる命題の使いやすい表現を得る助けとなることである」と説明している(p. 249)。

ここで注意すべきはideal element $\alpha$ は連言と選言のどちらか一方のように見なすことはできない。少し簡単にして上頂点2と下頂点2の例を考えよう。 $a_1\to b_1, a_1\to b_2, a_2\to b_1, a_2\to b_2$ からは最初に前件に選言を用いるのと後件に連言を用いるので、2通りの命題の組が得られる。

$a_1\lor a_2\to b_1, a_1\lor a_2\to b_2$
$a_1\to b_1\land b_2, a_2\to b_1\land b_2$

つまり $\alpha$ には $a_1\lor a_2$ と $b_1\land b_2$ のどちらも対応し得るのでどちらかを当てはめることはできない。

正直私は辺がほんの少し減るだけであるので、ideal elementを導入する利点がまったく理解できない。

しかし「ある要素を通過する」というアイデアは非常に良い着眼点であったと思う。それを今から説明しよう。

ここで我々はヘルツのテキストから離れて2個の要素から1つの要素への2個の矢印を彼のように考えてみよう。　

左図: $a_1\to b, a_2\to b$

これらをヘルツと同様にideal element $\alpha$ を考えると次の3つの射が得られる。

右図: $a_1\to \alpha$ , $a_2\to \alpha$ , $\alpha\to b$

これは圏論での余積の説明と似ていないだろうか?

射 $A\to X$ と $B\to X$ が与えられた時、余積対象を「通過するような」射が存在して図式が可換になる⁷。ヘルツの図を変形して書けば圏論の図式のようになる。同様に上頂点1かつ下頂点2の図式を考えると積対象のようになる。

繰り返すがヘルツが論理結合子を導入する目的はシステムに含まれる命題の個数を減らすためである。よって命題の個数が減らない場合に論理結合子を導入しようとすることはヘルツの意図に反し、ヘルツが最も単純なこのような場合を扱わなかったのはそのためだと思われる。

ideal elementが連言と選言のどちらかであるわけではないので、圏論的な説明が正確に対応するわけではない。しかし、複数の矢印が通過するような対象を考えるというアイデア自体は時代の先を行っていたのである。ヘルツのシステム内ではideal elementは積極的な役割を持たず、ヘルツがゲンツェンのようには重視しなかった点は惜しまれる。

参考文献

この記事に用いたヘルツの論文は以下のものである。

Über Axiomensysteme für beliebige Satzsysteme | SpringerLink

英訳含めネット上で読むことが可能である。

EUDML | Axiomensysteme für beliebige Satzsysteme. I. Teil. Sätze ersten Grades. (Über die Axiomensysteme von der kleinsten Satzzahl und den Begriff des idealen Elementes)

Universal Logic: An Anthology: From Paul Hertz to Dov Gabbay | SpringerLink

Part IIではより一般化され、変数を含む命題も扱われている。

https://www.deutsche-digitale-bibliothek.de/item/FUUS63FDVG6O56KST2NLKBH2ZOP23O4G

証明論的意味論のShroeder-Heisterは単一化と論理プログラミングの観点からヘルツと最初期のゲンツェンの結果について論じている。

Resolution and the Origins of Structural Reasoning: Early Proof-Theoretic Ideas of Hertz and Gentzen | Bulletin of Symbolic Logic | Cambridge Core

Arndt(2020)はヘルツのアイデアを利用し、ボトムアップに原子論理式を導入していくExplosion Calculus(爆裂計算)という新しい体系を定式化した。

The Explosion Calculus | SpringerLink

Gerhard Gentzen, Über die Existenz unabhängiger Axiomensysteme zu unendlichen Satzsystemen, Math. Ann. 107 (1933) pp. 329-350.
Mathematische Annalen - GDZ ↩
現代的な論理体系の定義との混同を避けるためシステムとカタカナで書き区別することにする。↩
このようなものはsemi-categoryと呼ばれているようである
semicategory in nLab ↩
特にこの解釈が含意を矢印として見なす観点と親和的である。ヘルツ自身が科学者であり、この解釈はscienceやcomputer scienceへの論理学の応用の先駆けの一つである。↩
厳密には論理結合子と呼ぶのは適切ではないかもしれないが、煩雑となるのでここではヘルツのものも論理結合子と呼ぶことにする。↩
ヘルツの論文の図に説明のために頂点にラベルを書き加えた。↩
coproduct in nLab ↩

Asinus's blog

西牟田祐樹のブログです。

射としての含意: Paul Herz, "Über Axiomensysteme für beliebige Satzsystem"を読む

ゲンツェンとの関係

射としての含意

分解対象としての論理結合子

参考文献